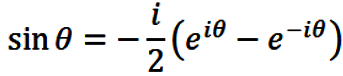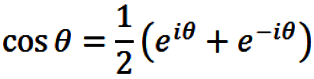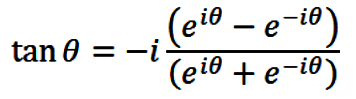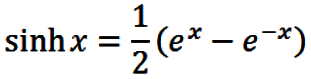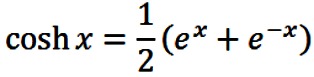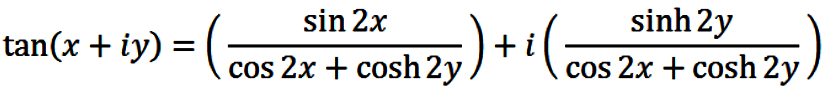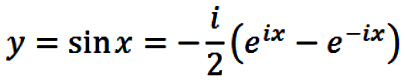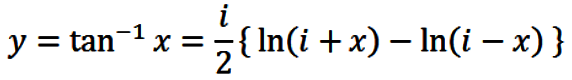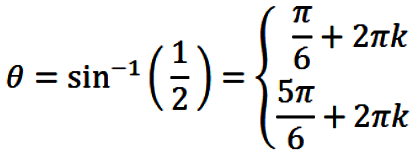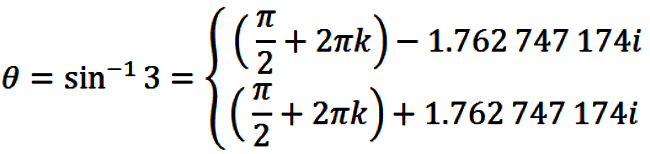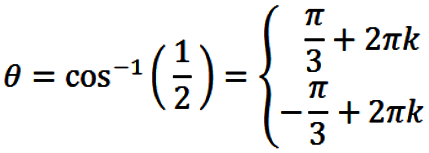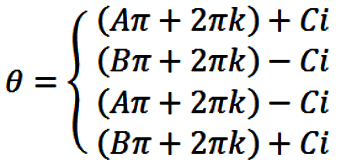Trigonometry

The Complex Valued Trigonometric Functions

Formulae in terms of Exponential Functions

Expressions for the complex valued trigonometric functions follow directly from Euler's formula

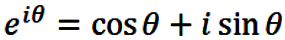(1)

and its conjugate

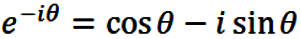(2)

Addition and subtraction of eqns. (1) and (2) yield the formulae for sine and cosine, i.e.,

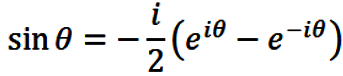(3)

and

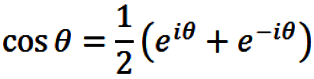(4)

Tangent is then obtained from the ratio of eqns. (3) and  (4), i.e.,

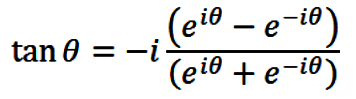(5)

Typically, θ in eqns. (1) and (2) is considered to be real valued, but it does not have to be. If we let θ = z where

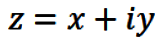(6)

and x and y are real, then for θ = z in eqns. (3) through (5), e^iθ and e^–iθ may be evaluated via

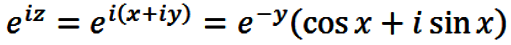(7)

and

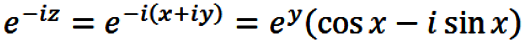(8)

Consequently, eqns. (3) through (8) define the (generally complex valued) trigonometric functions of complex valued arguments.

TI-84 Programs

The TI-84 calculator evaluates e to complex powers. Thus, eqns. (3) through (5) may be used to evaluate the trigonometric functions of complex argument with the TI-84. Simple TI-84 programs which do this are listed directly below:

• SIN.8xp
• COS.8xp
• TAN.8xp

Alternate Formulae, Periodicity and Graphs

With the aid of eqns. (7) and (8), the basic formula (3) through (5) may be expressed entirely in terms of real valued functions. The results presented below are in terms of the real valued sine and cosine, and the real valued hyperbolic sine and hyperbolic cosine, which are defined via

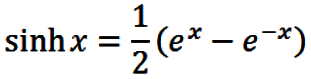(9)

and

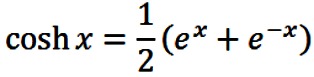(10)

Note that eqns. (9) and (10) and eqns. (3) and (4) imply sin(iy) = isinhy and cos(iy) = coshy.

Notwithstanding, using the well-known angle sum formula for sine, one obtains

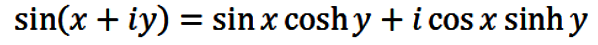(11)

which function still has period 2π.

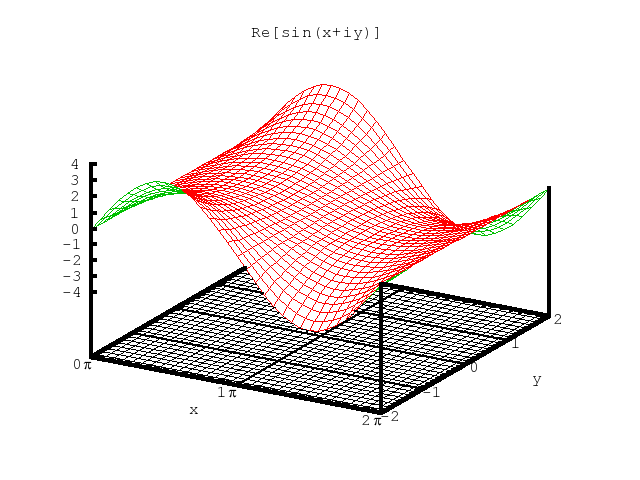Figure 1. The real part of sinz, i.e., sinxcoshy

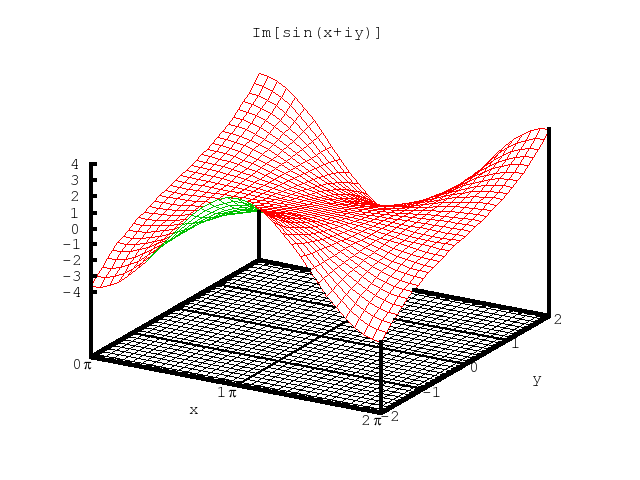Figure 2. The imaginary part of sinz, i.e., cosxsinhy

In a similar fashion, the angle sum formula for cosine yields

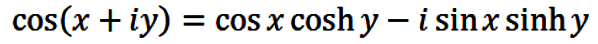(12)

which, again, still has period 2π.

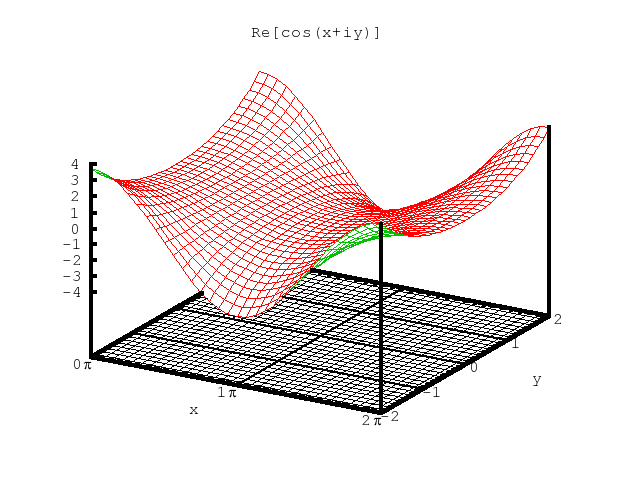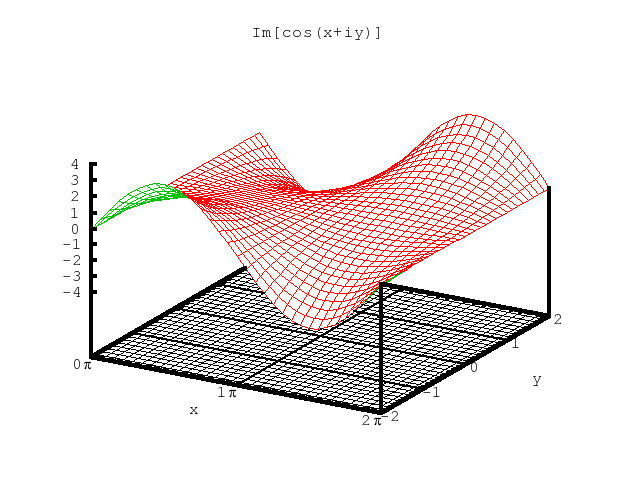
Figure 3. The real part of cosz, i.e., cosxcoshy

Figure 4. The imaginary part of cosz, i.e., -sinxsinhy

The case of the tangent function is much more complicated, and the details of derivation are omitted here. Suffice it to say that the angle sum formula for tangent, along with other identities involving the trigonometric and hyperbolic functions (which identities are omitted herein), yield, after a fair amount of algebra

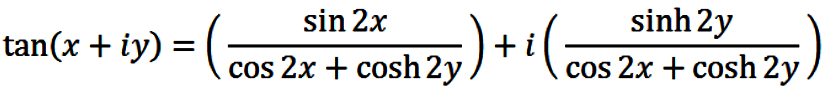(13)

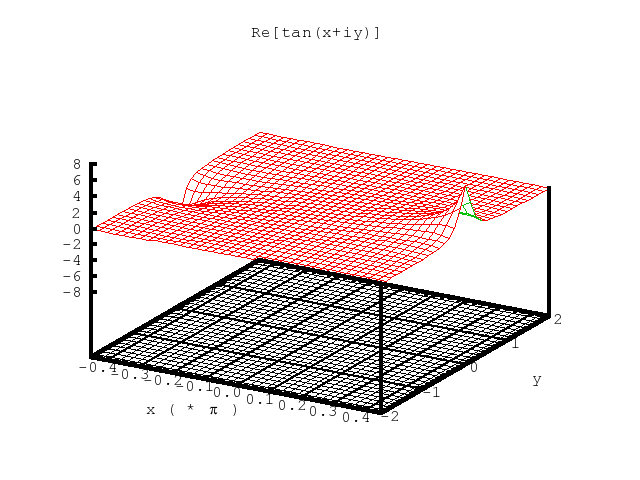
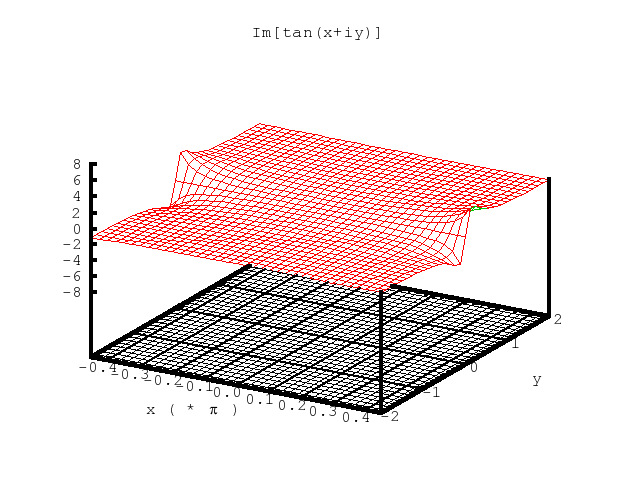
Note that the period here is π, and that the graphs shown below depict effectively one period, i.e., ‑0.45π < x < 0.45π.

Figure 5. The real part of tanz

Figure 6. The imaginary part of tanz

The Complex Valued Natural Logarithm

The formulae for the inverse trigonometric functions of complex argument depend on the complex valued natural logarithm, which function is described here.

First, write the complex number z in both rectangular and polar form:

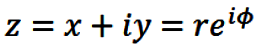(14)

where

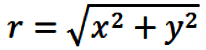(15)

and

(16)

Note that, in eqn. (16), the inverse tangent function returns a value of φ such that ‑π < φ ≤ π, depending upon the quadrant in which z resides. Next, taking the natural logarithm of eqn. (14) then yields the desired function:

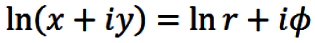(17)

The Complex Valued Inverse Trigonometric Functions

In order to find the formula for the inverse sine function, rewrite eqn. (3) as

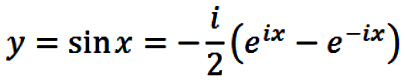(18)

which we want to invert, i.e.,

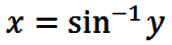(19)

Thus, multiply eqn. (18) by e ^ix to obtain the quadratic in e ^ix

(20)

whose solution for x is

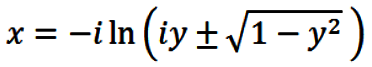(21)

Interchanging x and y in eqns. (19) and (21) then gives the desired formula

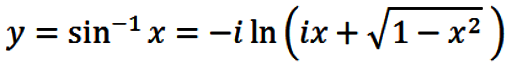(22)

where the plus branch of eqn. (21) was used in order for eqn. (22) to give the principal branch of the inverse sine function.

The derivations of formulae for inverse cosine and inverse tangent follow exactly the same procedure as just outlined above for inverse sine. One obtains

(23)

and

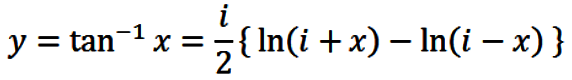(24)

both of which correspond to the principal branch.

Since x may be complex in eqns. (22) through  (24), these three equations define the (generally complex valued) inverse trigonometric functions of complex argument.

TI-84 Programs

The TI-84 calculator evaluates both natural logarithms and square roots of complex numbers. Thus, eqns. (22) through (24) may be used to evaluate the inverse trigonometric functions of complex argument with the TI-84. Simple TI-84 programs which do this are listed directly below:

• SININV.8xp
• COSINV.8xp
• TANINV.8xp

Examples

Example #1: Solve

(25)

for all values of θ.

SOLUTION:

Factoring eqn. (25) gives

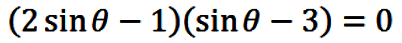(26)

so that

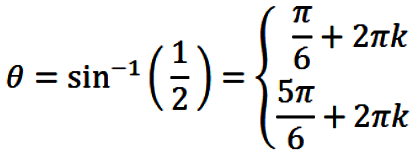(27)

and

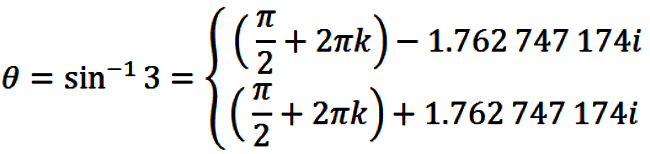(28)

where k can be any integer. In eqn. (27), the first solution is obtained from the principal branch, and the second solution is obtained from symmetry (for instance, via the unit circle). Similarly, in eqn. (28), the first solution is obtained from the principal branch, and the second solution is obtained from symmetry (cf., Figures 1 and 2 above).

Example #2: Solve

(29)

for all values of θ.

SOLUTION:

Factoring eqn. (29) gives

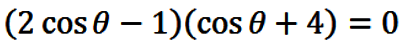(30)

so that

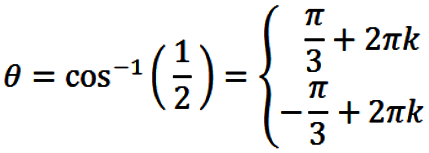(31)

and

(32)

where k can be any integer. In eqn. (31), the first solution is obtained from the principal branch, and the second solution is obtained from symmetry (for instance, via the unit circle). Similarly, in eqn. (32), the first solution is obtained from the principal branch, and the second solution is obtained from symmetry (cf., Figures 3 and 4 above).

Example #3: Solve

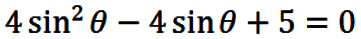(33)

for all values of θ.

SOLUTION:

Via the Quadratic Formula eqn. (33) gives

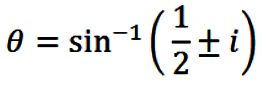(34)

so that

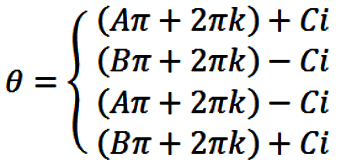(35)

where

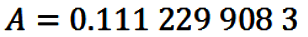(36)

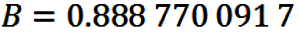(37)

and

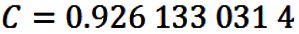(38)

Once again, in eqn. (35), k can be any integer. Note that the first and third solutions in eqn. (35) are obtained from the principal branches, and that the second and fourth solutions are obtained from symmetry (cf., Figures 1 and 2 above).