Steve's Sudoku

Free Sudoku Puzzles

The free Sudoku program is written in Java, so it will run on any operating system that supports Java, e.g., Windows, Mac, Linux, etc. The current version of the program is different than previous versions in that it has no expiration date, and that it will generate as many puzzles per day as one may want to solve. Each day that the program is run, a different sequence of puzzles will be generated. The current version of the program is also different from previous versions in that the game is now played on a graphical interface, as opposed to being played on a printed out puzzle. Nevertheless, you may still output the puzzles to your Desktop and print them, i.e., you may still play them with pencil and paper if you wish.

Additionally, a program Solve Sudoku, which solves Sudoku puzzles can be downloaded from this page.

A Sample from the Program

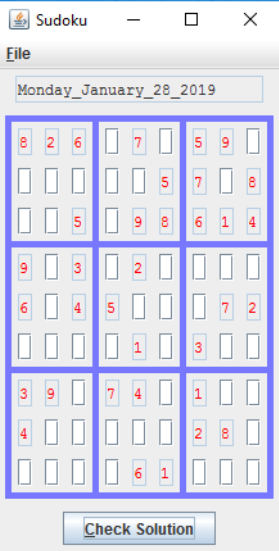
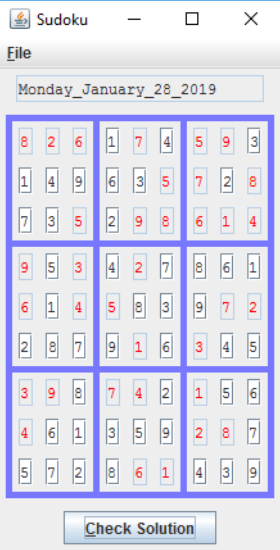
Here is an emply and filled out sample puzzle generated by the program.

The author would consider that the puzzles generated are of "Easy" to "Moderate" difficulty.

Installation Instructions

1. Click on the Sudoku.jar link below and download the file to your Desktop.
   
   
2. To run the program, double click on the downloaded "Java" icon. That's it!

Download

Sudoku.jar   (32,882 bytes)

Problems with the Program

If you run into any problems with the program, or if you have any comments about it, please e-mail the author at steve@harren.us.

Comments on Uniqueness of Solution

The Sudoku puzzles generated by the program have 35 clues, which the author has found always to generate solvable puzzles. In some instances, though, the solutions will not be unique, as described by the three cases below. Nevertheless, the author has found that this does not detract from the enjoyment of solving the puzzles.

Case I - Permutations of Two Numbers.

Fairly often, the program generates puzzles whose solution contains, in the grid, two numbers, say 1 and 2, which (validly) may be arranged two ways, e.g.,

      +-----+   +-----+              +-----+   +-----+
      |     |   |     |              |     |   |     |
      |  1  |   |  2  |              |  2  |   |  1  |
      |     |   |     |              |     |   |     |
      +-----+   +-----+     /__\     +-----+   +-----+
                            \  /
      +-----+   +-----+              +-----+   +-----+
      |     |   |     |              |     |   |     |
      |  2  |   |  1  |              |  1  |   |  2  |
      |     |   |     |              |     |   |     |
      +-----+   +-----+              +-----+   +-----+
          

Case II - Permutations of Three Numbers.

Rarely, the program will generate a puzzle whose solution contains, in the grid, two rows of three numbers, say 1, 2 and 3, with each row being contained within a different 3 by 3 cell. Such an arrangement also (validly) may be arranged two ways, via an even permutation of the numbers, e.g.,

      x-----+-----+-----x              x-----+-----+-----x
      x     |     |     x              x     |     |     x
      x  1  |  2  |  3  x              x  3  |  1  |  2  x
      x     |     |     x              x     |     |     x
      x-----+-----+-----x     /__\     x-----+-----+-----x
                              \  /
      x-----+-----+-----x              x-----+-----+-----x
      x     |     |     x              x     |     |     x
      x  3  |  1  |  2  x              x  1  |  2  |  3  x
      x     |     |     x              x     |     |     x
      x-----+-----+-----x              x-----+-----+-----x
          

Note that a similar situation may exist on a columnwise basis.

Case III - Three or More Valid Solutions.

When guessing is required to solve the puzzle generated, a valid solution can always be obtained, but in this case, sometimes three (or more) valid solutions can be identified. The author must admit that the mathematics of uniqueness of Sudoku solutions is highly complicated, an he is by no means an expert on the subject.